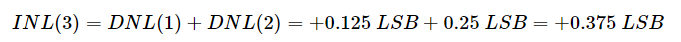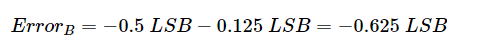上一篇我们介绍了ADC微分非线性(DNL)误差,今天继续介绍一下 ADC 积分非线性(INL)误差。本文您将了解到积分非线性(INL)规格指标及其与模数转换器 (ADC) 误差的关系。
失调误差、增益误差和积分非线性误差(INL)这三个参数决定了ADC的精度。失调和增益误差可以通过校准来减小,这使得INL成为主要的误差贡献者。INL规格描述了实际传递函数的过渡点与理想值的偏差。
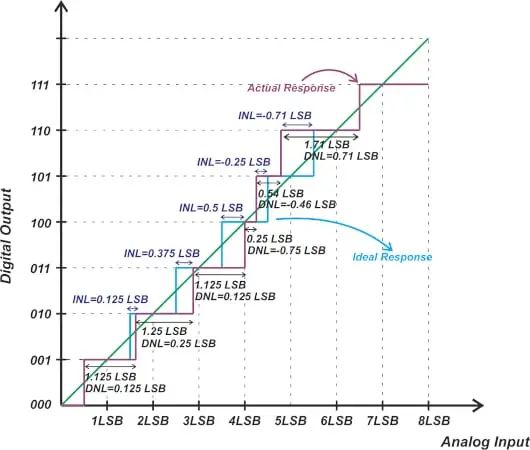
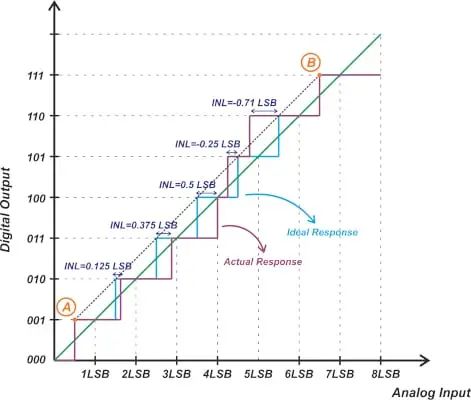
理想的ADC具有均匀的阶梯输入-输出特性,这意味着每次转换发生在与上一个转换相距1 LSB(最低有效位)处。但是,对于实际ADC,步骤并不统一。例如,考虑图1所示的传递曲线。步宽与理想值的偏差由微分非线性(DNL)规范表征。然而,DNL误差不能完全描述传递函数与理想响应的偏差,因为我们获得的响应取决于DNL正负误差在不同码字中的分布方式。INL 规范允许我们表征输出码字转换与其理想值的偏差。要计算码字 k 的 INL,我们可以使用以下等式:
其中 Ta(k) 和 Tideal(k) 分别表示从码字 k-1 到 k 的实际和理想过渡;“理想步长”是ADC的LSB。对于上述示例,从码字 1 (001) 到码字 2 (010) 的实际转换发生在理想转换上方 0.125 LSB 处。因此,码字 2 的 INL 是 INL(2) = +0.125 LSB。从这里开始,我们可能会问,下一个转换(从码字 2 到 3)呢?请注意,从码字 1 到 2 的转换发生在理想值以上 0.125 LSB 处,并考虑到码字 2 的宽度误差(或 DNL)为 +0.25 LSB,我们可以推断从码字 2 到 3 的转换应该发生在理想值以上 0.375 LSB 处。因此,我们有 INL(3) = +0.375 LSB。如您所见,码字 3 的 INL 等于码字 1 和 2 的 DNL 之和: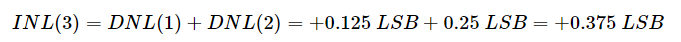
将上述分析扩展到其他码字,很容易通过应用以下等式来验证第 m 个码字的 INL:

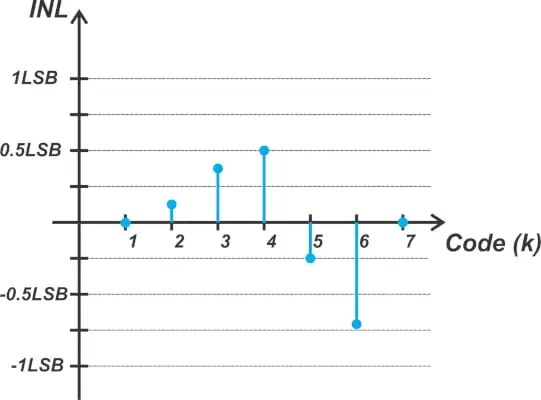
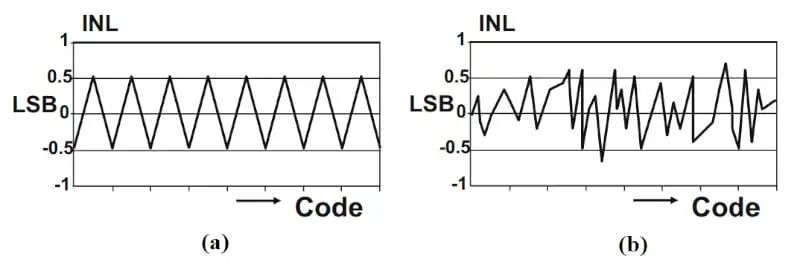
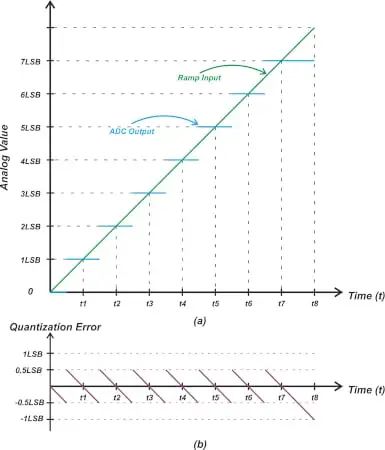
INL 表示 DNL 错误的累积影响。在计算DNL和INL值时,我们假设ADC的失调和增益误差已经校准出来。因此,第一个码字(码字 1)和最后一个码字的 INL 为零。对于码字零,未定义 INL。就像 DNL 一样,我们可以将 INL 信息表示为 INL 相对于码字值的图。对于上面的示例,我们得到如图 2 所示的下图。INL 通常也表示为所有码字的最小值和最大值。我们假设的ADC的INL介于-0.71 LSB和+0.5 LSB之间。INL图不仅表示ADC的线性度性能,而且还揭示了有关ADC内部架构的一些信息。例如,子范围ADC具有三角形INL图(图3(a)),而闪存ADC通常具有随机模式(图3(b))。图3.子范围ADC三角形INL图(a)和闪存ADC的随机模式图(b)示例。图片由 M. Pelgrom 提供 值得注意的是,INL是ADC量化误差之外的一个误差。由于ADC将连续的模拟输入范围转换为几个离散的输出码字,即使是一个理想的ADC也会在系统中引入一些误差,即量化误差。如果我们将一个斜率为1的斜坡输入到ADC,我们可以从输入中减去输出代码的模拟等效值,从而找到量化误差。这在图4中得到了说明。在图4中,绿色曲线表示斜坡输入,蓝色阶跃表示理想ADC产生的码字的模拟等效值。然而,图4中的下图显示了锯齿形状的量化误差。让我们看看非线性如何影响误差项。如果将斜坡输入应用于图1中的非理想特性曲线,则得到以下误差波形(图5)。图5. 示例图显示了ADC输出码字的模拟等效值以及理想变换(a)和误差波形(b)。图5(a)中的紫色阶跃表示ADC输出码字的模拟等效值,蓝点表示均匀阶梯响应的理想过渡点。例如,考虑从码字 1 到码字 2 的转换。如果这种转换发生在理想点(A点),则码字1的最负误差将是-0.5 LSB。由于 INL(2)=+0.125 LSB,因此从码字 1 到码字 2 的实际转换发生在高于理想值的 +0.125 LSB 处。由于这种延迟转换,绿色曲线与ADC输出之间的差值在转换点(B点)大于0.5 LSB。通过检查该图,您可以确认 B 点的误差由下式给出: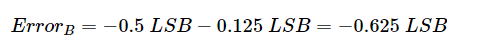
请注意,虽然这种非理想效应将码字 1 的误差扩展到 -0.625 LSB,但它将下一个码字(码字 2)的误差上限降低到 0.5 LSB - 0.125 LSB = +0.375 LSB。您可以在 D 点看到由 INL(3) = +0.375 LSB 引起的误差波形的类似变化。让我们检查码字 6,看看负 INL 如何影响错误 (INL(6 )= -0.71 LSB)。在这种情况下,(F点)处的实际跃迁发生在理想值(E点)以下0.71 LSB处。由于ADC输出增量早于预期值,因此会产生较大的正误差。如错误图所示,码字 6 的误差可以大到:
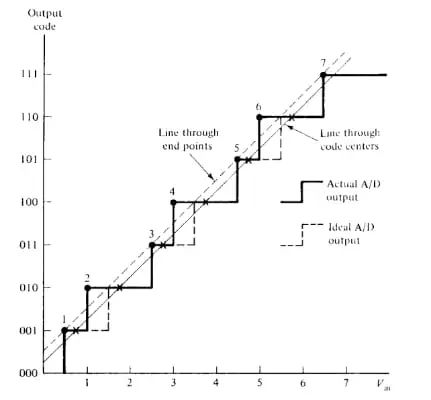
使用理想ADC时,量化过程会产生±0.5 LSB的误差。然而,对于实际的ADC,量化过程和INL都会影响系统的整体误差。换句话说,INL是超出量化误差的误差。到目前为止,我们考虑的INL定义可能是该规格指标中最有用和最常见的定义。但是,应该注意的是,ADC制造商的技术文档中有时会提到其他一些定义。为了避免任何混淆,我们将在本文的其余部分查看INL的其他常见定义。在我们继续其他定义之前,值得一提的是,人们可以用稍微不同的方式查看图 1 中使用的定义。与其将 INL 定义为码字转换与其理想值的偏差,我们可以将其定义为码字转换与经历第一个和最后一个码字转换的直线的偏差。如图 6 所示。在图 6 中,点 A 和 B 是第一个和最后一个转换点。由于我们假设在INL计算之前失调和增益误差为零,因此A点和B点对应于理想和实际传递函数。如您所见,穿过点 A 和 B 的线也穿过理想特性的所有其他过渡点(图中的蓝色曲线)。因此,实际过渡点与其相应理想过渡点的偏差等于该实际过渡点与穿过点 A 和 B 的直线的偏差。一些参考文献,如《高速模数转换》一书,使用此直线来定义ADC INL。另请注意,此参考线与之前文章中介绍的ADC线性模型(图中的绿线)不同。对于这种类型的定义,ADC传输特性是根据穿过ADC码字中心的直线定义的。图 7 显示了如何使用码字中心线定义 INL。图7.使用码字中心线定义 INL。图片由 R. Plassche 提供在上面的示例中,对角线是穿过理想ADC阶跃中点的线(我们在本系列的文章中称之为ADC的线性模型)。如图所示,实际步长中点与直线的偏差被视为该码字的INL误差。此示例显示了此定义的一个缺点。如您所见,码字 1101 的相邻转换偏离了理想值。但是,由于 1101 的测量码字中心与理想值一致,因此该码字的 INL 为零。使用图 1 中使用的定义,码字 1101 的 INL 将不为零。作为旁注,上面的图片取自Rudy van de Plassche的书。Rudy是世界著名的模拟设计师和许多电路和电路创意的发明者,例如斩波和稳定放大器,这些电路和电路理念在今天被广泛使用。图8.显示码字中心行定义的示例图。图片由M. Demler提供在这种情况下,用于计算INL误差的参考线是穿过实际传递函数的第一个和最后一个步骤的中点的线。对于三位ADC,这是穿过码字001和110中点的线路。实际步长的中点与这条直线的偏差被认为是该码字的INL误差。在这个特定的例子中,ADC传递函数具有交替的宽窄码字,从第一个和最后一个码字获得的参考线截获所有码字的中点。因此,所有码字的 INL 错误均为零。这再次凸显了基于码字中心的定义在某些情况下无法描述传递函数的非线性的缺点。本文中讨论的 INL 定义被归类为基于端点的定义,因为它们仅使用第一个和最后一个码字来派生参考线。定义 INL 误差的另一种方法是最佳拟合方法。在这种情况下,使用一条适合所有码字的直线作为参考线。本系列的下一篇文章将详细研究最佳拟合方法。https://www.allaboutcircuits.com/technical-articles/understanding-analog-to-digital-converter-integral-nonlinearity-inl-error/